Contact

Frequency Domain of Images – Fourier Transform and Filtering

frequential_donike
In [1]:
from skimage import io
from skimage import color
from skimage.restoration import denoise_nl_means, estimate_sigma

import numpy as np
from numpy.fft import fft, fftfreq, ifft

from scipy import ndimage as nd
from scipy.fft import fft, ifft
from scipy import fftpack

from PIL import Image, ImageDraw
import matplotlib.pyplot as plt
import time
import cv2
from math import sqrt
from math import exp

1.1 Load an image

In [2]:
img = io.imread("images/baseballdiamond08.tif")
plt.imshow(img)
plt.show()

1.2 Verify the invertibility of the FFT

In [3]:
# https://scipy-lectures.org/intro/scipy/auto_examples/solutions/plot_fft_image_denoise.html

# fft
img_fft =  fftpack.fft2(img)


# inverse of signal
img_ifft = fftpack.ifft2(img_fft).real

plt.figure(figsize=(10,10))

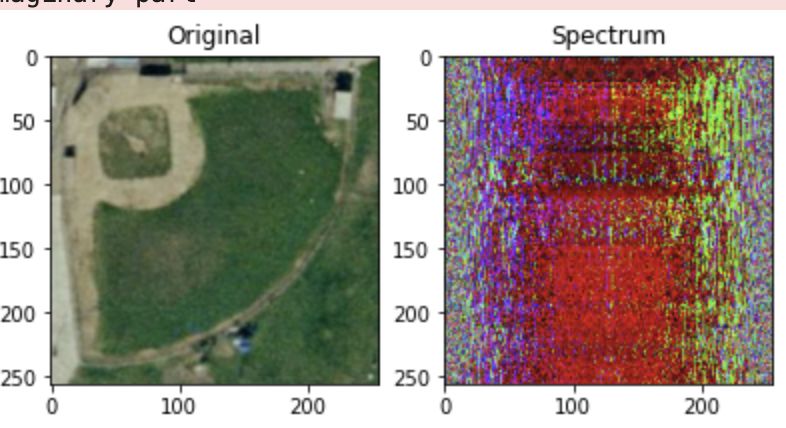
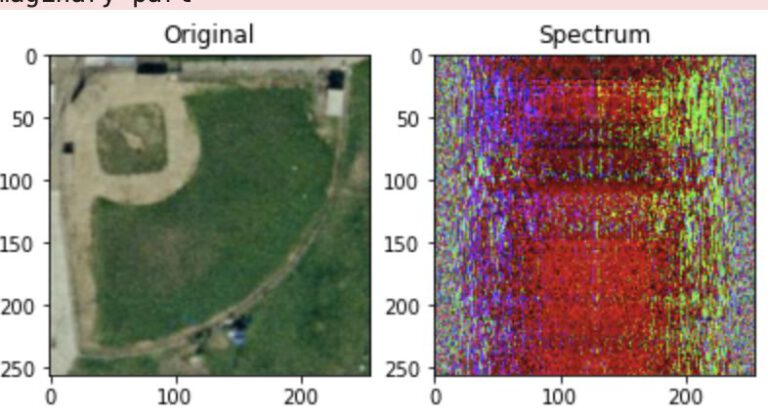
plt.subplot(131)
plt.imshow(img)
plt.title("Original")

plt.subplot(132)
plt.title("Spectrum")
plt.imshow(img_fft.astype(np.uint8))
plt.subplot(133)

plt.title("Reconstructed")
plt.imshow(img_ifft.astype(np.uint8))
plt.show()

/anaconda/lib/python3.7/site-packages/ipykernel_launcher.py:18: ComplexWarning: Casting complex values to real discards the imaginary part

The reconstruction based on the spectrum returns the original image.

1.3 Compare the effect of the main low-pass filters

Closely modeled (euphemism for copied) after this awesome Tutorial that helped me understand the process. Trying to implement these steps manually proved to be very difficult, with mixed/non-sensical results.

In [4]:
def rgb2gray(rgb):
    return np.dot(rgb[...,:3], [0.2989, 0.5870, 0.1140])
img = rgb2gray(img)

plt.imshow(img,cmap="gray")
plt.title("Gray")
plt.show()
In [5]:
plt.figure(figsize=(8, 6), constrained_layout=False)


img_fft = np.fft.fft2(img)
img_fftshift = np.fft.fftshift(img_fft)
img_ifftshit = np.fft.ifftshift(img_fftshift)
img_ifft = np.fft.ifft2(img_ifftshit)

plt.subplot(231), plt.imshow(img, "gray"), plt.title("Original Image")
plt.subplot(232), plt.imshow(np.log(1+np.abs(img_fft)), "gray"), plt.title("Spectrum, FFT")
plt.subplot(233), plt.imshow(np.log(1+np.abs(img_fftshift)), "gray"), plt.title("Centered Spectrum")
plt.subplot(234), plt.imshow(np.log(1+np.abs(img_ifftshit)), "gray"), plt.title("Decentralized IFFT")
plt.subplot(235), plt.imshow(np.abs(img_ifft), "gray"), plt.title("Reversed Image")

plt.show()
In [6]:
def distance(point1,point2):
    return sqrt((point1[0]-point2[0])**2 + (point1[1]-point2[1])**2)

def gaussianLP(D0,imgShape):
    base = np.zeros(imgShape[:2])
    rows, cols = imgShape[:2]
    center = (rows/2,cols/2)
    for x in range(cols):
        for y in range(rows):
            base[y,x] = exp(((-distance((y,x),center)**2)/(2*(D0**2))))
    return base
In [7]:
def try_d0s_lp(d0):
    plt.figure(figsize=(25, 5), constrained_layout=False)


    plt.subplot(161), plt.imshow(img, "gray"), plt.title("Original Image")

    original = np.fft.fft2(img)
    plt.subplot(162), plt.imshow(np.log(1+np.abs(original)), "gray"), plt.title("Spectrum")

    center = np.fft.fftshift(original)
    plt.subplot(163), plt.imshow(np.log(1+np.abs(center)), "gray"), plt.title("Centered Spectrum")

    LowPassCenter = center * gaussianLP(d0,img.shape)
    plt.subplot(164), plt.imshow(np.log(1+np.abs(LowPassCenter)), "gray"), plt.title("Centered Spectrum multiply Low Pass Filter")

    LowPass = np.fft.ifftshift(LowPassCenter)
    plt.subplot(165), plt.imshow(np.log(1+np.abs(LowPass)), "gray"), plt.title("Decentralize")

    inverse_LowPass = np.fft.ifft2(LowPass)
    plt.subplot(166), plt.imshow(np.abs(inverse_LowPass), "gray"), plt.title("Processed Image")

    plt.suptitle("D0:"+str(d0),fontweight="bold")
    plt.subplots_adjust(top=1.1)
    plt.show()
    
    
for i in [100,50,30,20,10]:
    try_d0s_lp(i)

1.4 Compare the effect of the main high-pass filters

In [8]:
def gaussianHP(D0,imgShape):
    base = np.zeros(imgShape[:2])
    rows, cols = imgShape[:2]
    center = (rows/2,cols/2)
    for x in range(cols):
        for y in range(rows):
            base[y,x] = 1 - exp(((-distance((y,x),center)**2)/(2*(D0**2))))
    return base
In [9]:
def try_d0s_hp(d0):
    plt.figure(figsize=(25, 5), constrained_layout=False)


    plt.subplot(161), plt.imshow(img, "gray"), plt.title("Original Image")

    original = np.fft.fft2(img)
    plt.subplot(162), plt.imshow(np.log(1+np.abs(original)), "gray"), plt.title("Spectrum")

    center = np.fft.fftshift(original)
    plt.subplot(163), plt.imshow(np.log(1+np.abs(center)), "gray"), plt.title("Centered Spectrum")

    HighPassCenter = center * gaussianHP(d0,img.shape)
    plt.subplot(164), plt.imshow(np.log(1+np.abs(HighPassCenter)), "gray"), plt.title("Centered Spectrum multiply High Pass Filter")

    HighPass = np.fft.ifftshift(HighPassCenter)
    plt.subplot(165), plt.imshow(np.log(1+np.abs(HighPass)), "gray"), plt.title("Decentralize")

    inverse_HighPass = np.fft.ifft2(HighPass)
    plt.subplot(166), plt.imshow(np.abs(inverse_HighPass), "gray"), plt.title("Processed Image")

    plt.suptitle("D0:"+str(d0),fontweight="bold")
    plt.subplots_adjust(top=1.1)
    plt.show()
    
    
for i in [100,50,30,20,10]:
    try_d0s_hp(i)

1.5 Perform image sharpening in the frequency domain

Add High-Pass to original to sharpen image.

In [10]:
d0 = 100

# perform FFT
original = np.fft.fft2(img)
# get spectrum
center = np.fft.fftshift(original)
# center spectrum for high pass
HighPassCenter = center * gaussianHP(d0,img.shape)
# perform high pass
HighPass = np.fft.ifftshift(HighPassCenter)
# reverse FFT -> IFFT
inverse_HighPass = np.fft.ifft2(HighPass)
# add filter to original image
sharpened = img+np.abs(inverse_HighPass)


plt.figure(figsize=(10, 10))
plt.subplot(121)
plt.imshow(img, "gray")
plt.title("Original Image")

plt.subplot(122)
plt.imshow(sharpened,cmap="gray")
plt.title("Sharpened Image with D0:"+str(d0))
plt.show()

1.6 Add some periodic noise in the frequential domain and apply notch filter to remove it

Unfortunately, I have to use a similar strategy again. Adding periodic noise from here and performing the noise remove adapted from here.

In [11]:
# https://itqna.net/questions/1742/how-generate-noise-image-using-python
def add_periodic(img):
    orig = img
    sh = orig.shape[0], orig.shape[1]
    noise = np.zeros(sh, dtype='float64')

    X, Y = np.meshgrid(range(0, sh[0]), range(0, sh[1]))

    A = 40
    u0 = 45
    v0 = 50

    noise += A*np.sin(X*u0 + Y*v0)

    A = -18
    u0 = -45
    v0 = 50

    noise += A*np.sin(X*u0 + Y*v0)

    noiseada = orig+noise
    return(noiseada)
periodic = add_periodic(img).astype(int)


plt.figure(figsize=(6,6))
plt.imshow(periodic,cmap="gray")
plt.title("Periodic Noise")
plt.show()
In [12]:
from scipy import fftpack
import numpy.fft as fp
w = 10
h = 10

im = img
F1 = fftpack.fft2((im).astype(float))
F2 = fftpack.fftshift(F1)
for i in range(60, w, 135):
    for j in range(100, h, 200):
        if not (i == 330 and j == 500):
            F2[i-10:i+10, j-10:j+10] = 0
    for i in range(0, w, 135):
        for j in range(200, h, 200):
            if not (i == 330 and j == 500):
                F2[max(0,i-15):min(w,i+15), max(0,j-15):min(h,j+15)] = 0

plt.figure(figsize=(6,6))
plt.title("Spectrum")
plt.imshow( (20*np.log10( 0.1 + F2)).astype(int), cmap=plt.cm.gray)
plt.show()


im1 = fp.ifft2(fftpack.ifftshift(F2)).real
plt.figure(figsize=(6,6))
plt.title("Recovered Image")
plt.imshow(im1, cmap='gray')
plt.show()

/anaconda/lib/python3.7/site-packages/ipykernel_launcher.py:20: ComplexWarning: Casting complex values to real discards the imaginary part

2.1 Load Grey Image

In [13]:
# local import
from add_noise import add_noise
?add_noise

Signature: add_noise(noise_typ, image)
Docstring:
Adds Noises:
- gaussian
- saltpepper
- speckle
- poisson
File:      ~/CDE_UBS/Image_Analysis/04_Frequency_based/add_noise.py
Type:      function
In [14]:
img = io.imread("images/baseballdiamond08.tif")
gaussian = rgb2gray(add_noise('gaussian',img))
saltpepper = rgb2gray(add_noise('saltpepper',img))
poisson = rgb2gray(add_noise('poisson',img))
speckle = rgb2gray(add_noise('speckle',img))
img = rgb2gray(img)

/home/simon/CDE_UBS/Image_Analysis/04_Frequency_based/add_noise.py:28: FutureWarning: Using a non-tuple sequence for multidimensional indexing is deprecated; use `arr[tuple(seq)]` instead of `arr[seq]`. In the future this will be interpreted as an array index, `arr[np.array(seq)]`, which will result either in an error or a different result.
  out[coords] = 1
/home/simon/CDE_UBS/Image_Analysis/04_Frequency_based/add_noise.py:33: FutureWarning: Using a non-tuple sequence for multidimensional indexing is deprecated; use `arr[tuple(seq)]` instead of `arr[seq]`. In the future this will be interpreted as an array index, `arr[np.array(seq)]`, which will result either in an error or a different result.
  out[coords] = 0
In [15]:
plt.figure(figsize=(25, 5))
plt.subplot(151)
plt.imshow(img, cmap='gray')
plt.title('original image')
plt.subplot(152)
plt.imshow(gaussian, cmap='gray')
plt.title('Gaussian Noise added')
plt.subplot(153)
plt.imshow(saltpepper, cmap='gray')
plt.title('SaltPepper Noise added')
plt.subplot(154)
plt.imshow(poisson, cmap='gray')
plt.title('poisson Noise added')
plt.subplot(155)
plt.imshow(speckle, cmap='gray')
plt.title('speckle Noise added')
plt.show()
In [16]:
# Median Filter on S&P Noise
saltpepper_filtered = nd.median_filter(saltpepper, size = 3)

plt.figure(figsize = (12,10))
plt.subplot(121)
plt.imshow(saltpepper,cmap="gray")
plt.title('S&P Noise')
plt.subplot(122)
plt.imshow(saltpepper_filtered,cmap="gray")
plt.title('S&P Noise Median Filtered')
plt.show()
In [17]:
# Median Filter on Speckle

speckle_filtered = nd.median_filter(speckle, size = 10)

plt.figure(figsize = (12,10))
plt.subplot(121)
plt.imshow(speckle,cmap="gray")
plt.title('Speckle Noise')
plt.subplot(122)
plt.imshow(speckle_filtered,cmap="gray")
plt.title('Speckle Noise Filtered')
plt.show()
In [18]:
# Gaussian Noise Filter
# get gaussian sigma
sigma_est = np.mean(estimate_sigma(gaussian))
# denoise based on
denoise = denoise_nl_means(gaussian, h =5*sigma_est, fast_mode = False, patch_size = 7, patch_distance =4)


plt.figure(figsize = (12,10))
plt.subplot(121)
plt.imshow(gaussian,cmap="gray")
plt.title('Gaussian Noise')
plt.subplot(122)
plt.imshow(denoise,cmap="gray")
plt.title('Gaussian Noise Filtered')
plt.show()
In [ ]:
Further Reading
Recent Updates